匀变速直线运动中位移与面积的关系及位移公式推导_J9九游会-真人游戏第一品牌

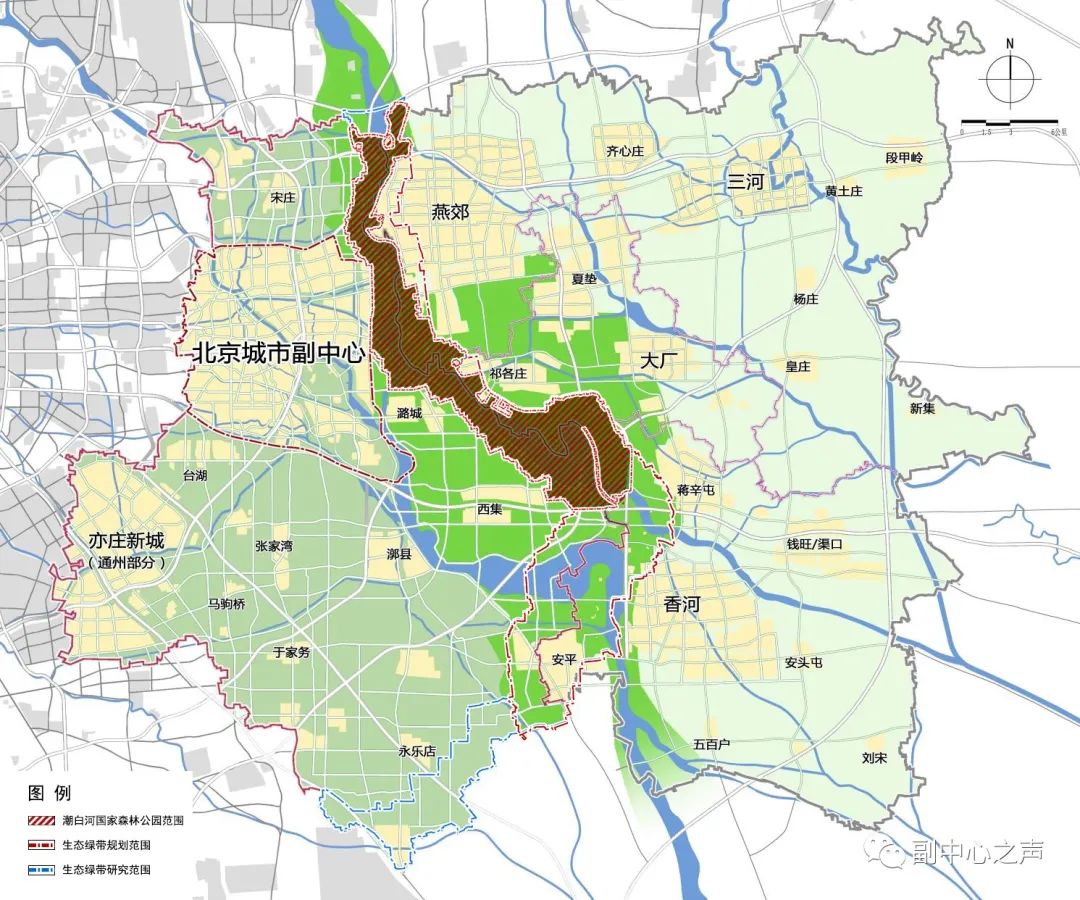
v - t 图像与位移关系基础

在匀变速直线运动的v-t图中，时间轴与图形所围成的梯形区域，实际上对应着物体的位移。比如，如果一辆小车正做匀变速直线运动，其v-t图中的某段图形是梯形，那么我们就可以直观地观察到梯形面积与位移之间的联系。这对学习直线运动非常关键，因为它把抽象的位移概念变得具体，使我们能更清楚地认识到运动过程中位置的改变。

在实验中，我们借助打点计时器等工具对小车的运动进行记录，并制作了速度与时间的关系图。通过观察图表，我们能够清楚地看到图形的形态。随着实验数据的累积，大家会发现梯形的面积值与实际位移的数据非常接近，这一发现有力地证实了理论的正确性。

位移时间公式推导

基于v-t图像，我们得出了位移随时间变化的公式。一般情况下，一辆小汽车从某一初始速度出发，若是在加速或减速，那么它在v-t图像上所覆盖的阴影部分面积，就等同于其位移。通过应用梯形面积的计算方法，我们可以计算出位移x，其公式为x等于v₀与v的平均值乘以时间t的一半。随后，将速度公式 v = v₀ + at 带入等式，我们逐步展开计算，最终得到 x = v₀t + 1/2·at²。在物理学的学习过程中，这种逐步的推导方法至关重要，因为它能让我们更深入地理解公式的本质。

这项练习需要我们依据汽车起始速度、加速情况和行驶时长来推算其位移。通过逐步应用推导公式，同学们能熟练掌握相关公式，并体会到其在现实中的实用意义。通过将理论与实际相结合，我们对公式有了更深刻的理解。

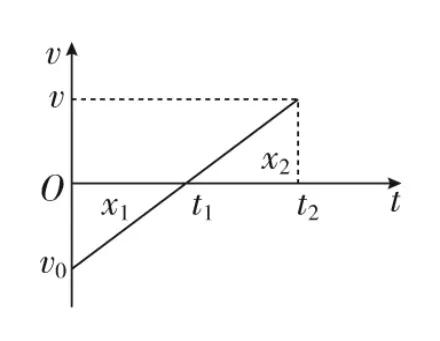
图像正负面积表示位移

图线若在时间轴之上，所形成的图形面积即被认定为正，这显示了物体的移动方向是向前的。以物体沿直线前进为例，若其v-t图线处于上方，便说明物体正在前进。这一现象揭示了物体实际运动的方向与图像面积的正负是相联系的。在时间轴之上计算位移较为直接，我们能够依据先前提到的公式和面积的概念来进行求解。

当图线处在时间轴的底部时，它的面积会变成负数，位移也会显示为负值。比如，物体在向后移动时，它的v-t图线就会位于下方。若物体的移动路径与时间轴有交点，那么总位移可以通过计算图线上下部分面积的总和来确定。比如，物体先前进再后退，其v-t图线会穿过时间轴，这时计算总位移就可以用这个方法。

位移公式特点剖析

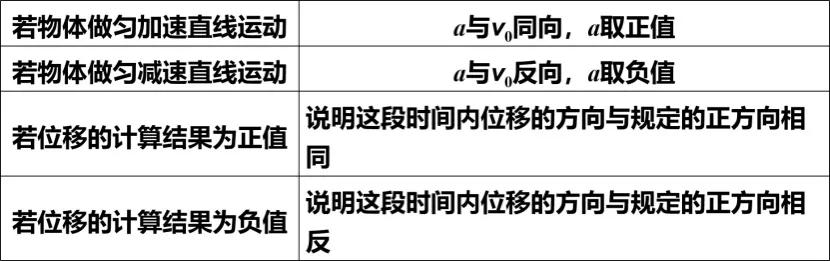
位移的计算公式是 x = v₀t + 1/2·at²，这个公式用于确定位移，它与路程的计算方式并不相同。位移和路程只有在物体沿一个方向直线移动时才会相等。比如，一个滑块在光滑的水平轨道上向一个方向滑动，它的位移和路程就相等。但如果滑块在移动过程中改变了方向，那么位移和路程就会不同。因此，在使用位移公式时，必须明确区分位移和路程这两个概念。

公式中矢量属性明显，时间t除外，其余均为矢量。我们常将初始速度朝向定为正向，使得x轴、加速度及初速度v₀同向。比如汽车加速，若以初速度方向为基准，加速度与位移均为正。解题时，一旦确定正方向，便可知各量正负，进而准确计算。

公式适用范围和特殊形式

公式x = v₀t + 1/2·at²只适用于匀变速直线运动，不能用于非匀变速。比如过山车，速度变化多端，不能用这个公式来计算位移。所以，判断物体是否做匀变速是使用这个公式的基础。我们必须通过测量速度和时间的变化，来核实加速度是否稳定不变。

位移公式的应用思路和刹车问题处理

解题步骤如下：首先确定研究对象，判断其是否进行匀变速运动。以火车进站为例，观察其速度是否均匀变化。然后，辨别已知与未知数据，找出初速度、加速度、时间和位移的具体数值。初速度即运动起始时的速度。接下来，设定一个正方向，将数值代入公式进行计算。按照这些步骤进行解题，有助于保持解题思路的清晰，减少出错的可能性。

以汽车为例，若汽车在特定速度下进行制动，并且设定了较长的制动时间，但车辆实际上已经停稳，此时我们应依据车辆从开始刹车到完全静止所花费的时间来推算其移动的距离。

关于匀变速直线运动的位移公式，你是否还有困惑？若这篇文章对你有所启发，不妨点个赞，或者分享给更多人看看。